Drafts

@cm3 の草稿置場 / 少々Wikiっぽく使っているので中身は適宜追記修正されます。

■

駄文

「博物館が特色を出す → 万人のためのものではなくなる → 来ない人のために何ができるか」という議論を耳にした時の違和感を言語化するために書き始めたメモ。

  • そもそも大学教育だって個々の分野を取れば直接万人のためのものではない（まあ、学部教育レベルくらいはオンライン無料で万人に提供されてていいと思うけど）
  • 宇宙際タイヒミュラー理論の解説がNHKで放映された際に、望月教授への取材について「宇宙際タイヒミュラー理論が今までの数学と何が違うのかを理解するには、高度な数学的知識が必要とされ、一般の視聴者どころか、一般の数学者でも理解困難ですので、取材はお断りさせて頂きます」（大意）という形で断られた件に対して「説明する責務がある」と、数回輪廻しても理解できなさそうな脳を晒しているtwitterアカウントが呟いているの見てマジvomitした
  • OAISが「指定コミュニティ」に引き継ぐという想定をするのも、どの空間、コミュニティを切り取ってもその知識が無いといけないなんて想定はただ無意味だからでしょう

NHKで放映されていた望月教授のメール

あたりが連想されて、博物館情報をオープンにすることだったり、それに基づく市民科学を推進すること自体は大賛成というかその旗を振らなきゃいけないくらいの立場の自覚はあるけど、その理路はちょっと危険だなと思った。「博物館が特色を出す → 万人のためのものではなくなる」の関係自体は重々意識しなきゃいけないことで、印象にのこったというのもあるんだけど、僕はこれをオープン化の理路にするのを意識的に避けなければと思った。つまり、

  • 特色というのが専門性ならば、それによって来なくなる人に対して、オープン化は処方箋になっていない。
  • 万人を対象にすることを志向することが、過度に求められること自体への危惧。

があった。ここで２つの問題が立つ。

  • 実際に活動として行われている博物館のオープン化は、どのような理路で、どのようなやり方で実施されるべきか
  • 博物館は、それぞれ、もしくは群として、万人のためのものであるべきか、そうでないとすれば、その存在価値は何に基礎づけられるか、それによってどのような範囲にどういう形で情報を届けなければならないか。

オープン化の理路として有名なものに NIHのポリシーの背景になった The Alliance for Taxpayer Access とかが使ってた「税金で運営してるんだから、その分還元されなきゃいけないでしょ」があって、これはこれで「お金払った人に特別に見せてあげる文化情報」みたいなのが跋扈する恐れみたいなのがあって、一理あるけど危なっかしいなぁと思ってる。アクセスの平等とか大事だよねみたいなのは、地域資料継承支援事業 - 基本方針 とかで出してる。

という形でも言及してたように、25条的な文脈で、情報市民権保障として設計するというのが他のやり方で、これは必ず必要だと思うんだけど、「ミニマム」「最低限度」をどのように測るか設定するかというのが難しい。最低限度を超えた範囲は経済に任すということになるんだけど、特に25条的立ち位置 vs 経済の関係については図書館がずっとその批判にさらされ答えてきているので（cf. 図書館の公共性批判への反論: ほどよい司書の日記 15年前くらいのブログ記事）まあ、それは参考になるかな。博物館の場合、基本的に一点物なので、財を通した民業との対立というより、公立 vs 私立の関係、入館料 vs 税金負担の関係が主になるという点で異なる。後者は本来無料な入館料を取ってる問題 (cf. 瀧端 真理子: 日本の博物館はなぜ無料でないのか？──博物館法制定時までの議論を中心に──）とも関連する。図書館での迷惑行為と入館禁止処分の件（ 図書館での迷惑行為と入館禁止処分～岐阜地裁判決 : 長野第一法律事務所　ブログ《分野別/信州の記事》 → 図書館利用禁止は「適法」、岐阜　大量借り出し巡り（共同通信） - Yahoo!ニュース）は判決が揺れたけど、「一部の利用者による不適切な負担を避ける」のも大事だと思う。結局この「適切」さが難しいんだけど。障碍者対応のコストはもちろんできるかぎり負うべきなんだけど、程度にもよるだろうし。ウェブ上なら、SPARQLエンドポイントはSPARQL書ける人だけがめっちゃ恩恵受けれる、キーボード打てる人は普通の検索窓で普通の検索はできる、3Dモデルは購入してください、云々、オープン化は情報市民権保障を中心として税金分の還元やより広いアクセス提供のために行われる。取りこぼしなく万人ってのは情報市民権保障から必要になるし、「一部の利用者による不適切な負担を避ける」のは税金分の還元から出てくる。

高等教育のマス化は私立セクターの増大によって達成された

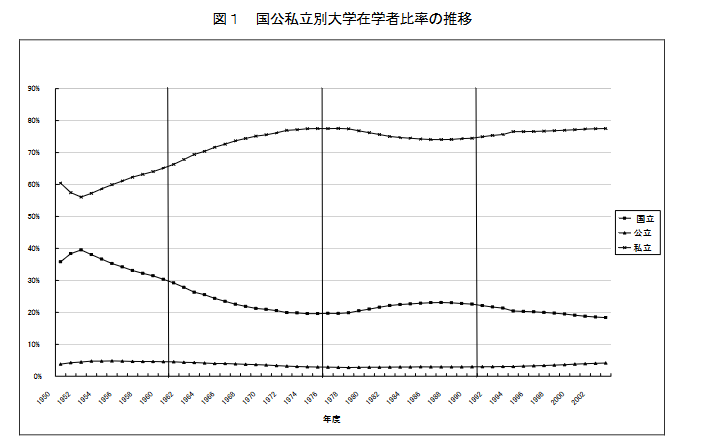
from 小林雅之: 国私格差是正と私学政策

日本の高等教育は私的負担が重い

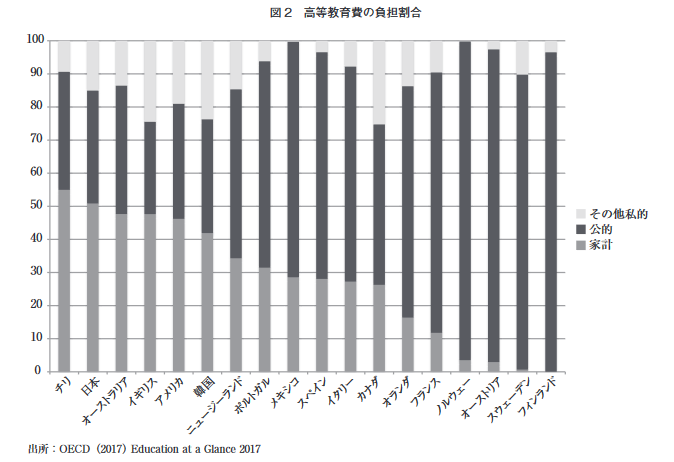
from 小林 雅之: 高等教育費負担の国際比較と日本の課題

国際比較したところで、イギリスが無料にしてるんは他国から収奪したものの展示の正当化みたいな側面もあるってのはそれはそうだし、こんだけ色々貧困になった国で先進国並みの文化政策をしようってのに無理があるというのもそれはそうだし、結局日本的な正当性ってのは私たち国民が決めるしかないのだけれど、昨今の政治状況を見るに、私たち国民が決める＝ポピュリズム的に決定するということになってしまう。ここでポピュリズムを民主主義と区別して用いているのは あなたは｢ポピュリズムと民主主義の違い｣をひとことで説明できるか 安倍政権の問題とは何だったのか | PRESIDENT Online（プレジデントオンライン） あたりでも触れられている、分かりやすい敵を作ること、熟議を軽視し少数派を「無視」する多数決を民主主義と思っていること、あたりを念頭に置いている。国立博物館の常設展を無料化しない本当の理由は何ですか？... -... - Yahoo!知恵袋 の中で、「『文化行政が云々』と、能書きをタレるくらいなら、震災の被災地で、ボランティアでもすれば」とかまったくロジックとして成立していなくても、共感されてしまえば、通ってしまう。

「博物館は、それぞれ、もしくは群として、万人のためのものであるべきか、そうでないとすれば、その存在価値は何に基礎づけられるか」について、冒頭に話を戻すと、「博物館が特色を出す → それぞれは万人のためのものではなくなる」このこと自体がそもそも現在の政治状況の中で劣勢を宿命づけられてしまうからしゃーなしに「→ 来ない人"に存在意義を認めて頂く"ために個々が直接万人の為ではあり得ない博物館に何ができるか」を考えなければならないとすれば、そのために情報のオープン化とかはあまり答えになっていない（どうせそれを活用するのはほんの一部の人々だから）。そもそもに「特色を出す」こと自体はある種の専門性を提供することを考えれば所与に近い話だから、博物館群全体としてのバランスを論じる必要はあるにせよ、個々が万人のためではないことは問題にならないはずで、群全体としても取りこぼすような人々についての問題だけが「→ 来ない人"に存在意義を認めて頂く"ために個々が直接万人の為ではあり得ない博物館に何ができるか」において考えるべき対象だ。各館レベルでもそれなりの人々に理解可能なコンテンツを提供する努力をするのは前提で、その「理解可能性」にも限界があるし、また、他にも色んな側面があるので、常に万人のためのものではない。

活用ばかりに重点が行っているという反対討論 もあった新博物館法に関して答申は真っ当。

博物館法制度の今後の在り方について（答申）より

① 資料の収集・保存と文化の継承（「守り、受け継ぐ」）

博物館は、自然と人類に関する有形・無形の遺産を、関連する事項を含め て地域や社会から資料として収集し、損失のリスクから確実に守るととも に、調査研究によって資料の価値を高め、未来へと継承する。

② 資料の展示、情報の発信と文化の共有（「わかち合う」）

博物館は、資料を系統的に展示し、デジタル化し、来場者のみならず広く 情報を発信することにより、共感と共通理解を醸成するなど人びとと文化 を共有する。

③ 多世代への学びの提供（「育む」）

博物館は、生涯学習・社会教育の拠点として、多世代の人びとへの学びの 機会を提供し、現在と未来に生きる世代を育む。

④ 社会や地域の課題への対応（「つなぐ、向き合う」）

博物館は、幅広い文化芸術活動をはじめ、まちづくりや福祉、国際交流、 観光、産業、環境などの関連団体、関係者とつながりながら、社会や地域 における様々な課題に向き合い、解決に取り組むことにより、持続可能な 地球環境の維持、創造的で活力ある地域社会づくり、人びとの健康で心豊 かな生活に貢献する。

⑤ 専門的人材の確保、持続可能な活動と経営の改善向上（「営む」）

博物館は、博物館を取り巻く幅広い業務に従事する様々な専門的人材を確 保するとともに、物的、財源的な基盤を確保し、安定した経営を行うこと によって持続して公益の増進を図る。また、使命の達成をめざし、評価・ 検証することにより、その活動と経営を改善し、価値を最大化させる。

まあ、価値の基礎はここらへんで合意しておけばいいし、博物館群としてある程度万人を対象にって感じかな。これらは or じゃなくて and で、各館の認定条件の大枠になるって言ってるんだから、「来場者のみならず広く情報を発信する」「多世代の人びとへの学びの機会を提供し」あたりは対象をなるべく幅広くという意識があって、これは博物館群じゃなくて個々の博物館でも満たさなきゃいけないということになる。なんぴとも排除してはならない、広いに越したことはない、くらいは言えて、なんぴとでも利益を享受できるようにしろ、は言っちゃいけないというのが

  • 万人を対象にすることを志向することが、過度に求められること自体への危惧。

の具体化になる。税金分の還元からの「一部の利用者による不適切な負担を避ける」話や情報市民権保障を博物館群全体としてサステイナブルにするための制約というのが意識されなければならない。

あとは、この価値観から零れ落ちる、もしくは（能力的に？）あまりにそれを享受できない人々に存在意義を認めて頂く方法かぁ。具体的にいうと、「公金を入れないと成り立たないのは文化ではない」と言っちゃう橋下徹やその支持者とかに認めさせる方法かな。（cf. 橋下は、日本の文化を何と考えているのか。—文楽助成金削減問題 : あちたりこちたり）もちろん、「存在意義を認めて頂く」は十分多数であればポピュリズム的にも問題が無いので小さい勢力ならば無視すれば良い（というのが reflexive な logic な）のだけど、そのポピュリズム本家本元の勢力だよね。「伝統芸能やクラシック音楽などの、いわゆるハイカルチャーに否定的な見解を示す一方、お笑い、ギャンブルやストリップなどの大衆文化を肯定的に評価する発言が多い。 」ってjawpに書かれてるけど、敵としての文化上流層みたいなのを設定しているという認識。ちなみに、個人的に、ギャンブルやストリップは僕も文化性を認めるんだけど、「お笑い」はマジで笑えたことないので、皆が認めるなら認めるけど…って感じです。一つは博物館鑑賞や図書館利用を初等教育に取り入れるというのはあって、欧米の博物館いくと常に小学生がツアーして学んでいるイメージがある。あとは代替医療とか「土偶を読む」問題と同じで、ルサンチマン問題だな。超人になればいい、なんて解決策でも何でもないので、「考え続けること」や「議論し続けること」に触れる機会を用意するしかないと思う。それが思考停止的な様式を持つポピュリズムへの処方箋にもなるんだろうから。

あと、そこからドロップアウトしたときに、闇落ちしない方法を用意すること。そのためにやさしくおしえてあげること。

ドメインを手放した時にlet's encryptの設定削除でやるべきこと on Ubuntu

一応以下の作業はサーバの停止、つまり、

service nginx stop

service nginx start

でサンドウィッチしてあげておくとよい。（nginx を前提に以下書いています。certbot のコマンドは apache も共通だけど）

さて本題。sudo で、

certbot revoke --cert-path /etc/letsencrypt/archive/${YOUR_DOMAIN}/cert1.pem

certbot delete --cert-name ${YOUR_DOMAIN}

をすればよい。ちなみに、既にドメインが失効している場合、revoke で

An unexpected error occurred: The client lacks sufficient authorization :: Certificate is expired

というエラーが出るので、単に delete だけでよい。

最後に

certbot certificates

をして、思ったものがでるか確認する。

さらにサーバの設定ファイルで該当箇所を削除する。include 構文でドメインに関わる記述をまとめておくと、一行コメントアウトするだけで済むので楽だね。

nginx -t

で設定ファイルにエラーが無いか確認して

nginx -s reload

で反映。冒頭でも書いたが、サーバを止めて作業していると思うので

service nginx start

を忘れずに。

ちなみにどんなドメインをなぜ手放したか。

研究プロフィールのためのドメインを2000円一生でもたかだか10万円にはおさまるだろうと取ってみたが、あまり使わなくてメンテもしていなかったし、Researchmap が十分普及したと判断したので、手放した。就活の際にはポートフォリオを持ちたい気分もあるが github pages とかで十分だろう。

参考記事

0.999…≠1な世界について

tl;dr

アルキメデスの公理、デデキントの公理、Weierstrassの公理 など実数の連続性を基礎づける６つの方法は相互に等価で、それらに極限の定義を加えることで、普段我々が触れている 0.999…=1な世界は作られている。それらの前提をある形で否定することで、「0.999…≠1な世界」を得ることができ、例えば、無限小を値として存在させる超準解析の世界が、その一つとして体系立てられている。超準解析の世界でも、これまでの数学の多くの理論を成立させることができ、また新たな理論の開拓を可能にしている。

まず、0.999…=1 だと証明するときは基本的に \lim_{n \to \infty}{\frac{1}{10}^n} = 0 に帰着させる。 これについて ε-N 論法は

「任意に与えられた正の数 ε \gt 0に対して、次のような番号 n_0 \in \mathbb{N} が存在すること。番号 n が n \geq n_0 を満たすならば、\frac{1}{10}^n \lt εを満たす」

となる。まず、この証明について、n_0 を見つけこそすれば、n \geq n_0 な n について満たすのはすぐに証明できるので、n_0 の存在だけがまずキーになる。lim 1/n=0はなぜ？ ε-n_0論法とアルキメデスの性質 | 趣味の大学数学 とかだと、アルキメデスの性質から、1 \lt εn となる自然数n_0 が存在、という説明をしている（たぶんこれが一番シンプル）。

さて、ここで少し違うコトを証明する。

a_n: {\frac{1}{10}^n} (n \in \mathbb{N}） に最小元 a_m \gt 0が存在すると仮定する。ここで、a_{m+1} = \frac{a_m}{10} \lt a_m （∵ 0 \lt a_m ）よって矛盾するので、背理法により、最小元 a_mは存在しない。

最小元と極限は別物であることが分かる。 ε-N 論法も外部から持ち込まれているし、アルキメデスの性質だってそうだ。つまり、アルキメデスの性質を満たさないものを考えたり、ε-N 論法以外の極限の定義の仕方をしたりすると、別の結論を得られそうなことはここから推測できる。

その具体例を見てみよう。

上記の、実数をそれぞれの小数展開に帰着させる方法は、フレッド・リッチマン (Fred Richman) によって雑誌 Mathematics Magazine に投稿された "Is 0.999… = 1?" という解説論文による説明である。この論文は大学の数学教師とその生徒向けに書かれている。リッチマンは、有理数の任意の稠密な部分集合における切断を考えても同様な結果をもたらすことを指摘している。その中で彼は、分母が 10 の冪である分数全体の成す稠密部分集合を用いて、0.999… = 1 の証明をより直接的に与えている。また、x < 1 となる x は切断を有するが、x ≤ 1 となる x は切断をもたないことも指摘し、「これは 0.999… と 1 が異なってしまうことを排除するものである。……実数の伝統的な定義の中に、等式 0.999… = 1 は最初から組み込まれている」と評した。リッチマンは、この手順に修正を加えることで、0.999… ≠ 1 となる別の構造を導いている。

from 0.999... - Wikipedia この別の構造を説明する。

論文は Is 0.999… = 1? で、「デデキント切断」の章にこの話が書いてある。

デデキント切断は通常、有理数環で定義される。しかし、十進数（ decimal numbers ）に興味があるのなら、有理数環とは別の環にこれを適用したいと考えるだろう。

有理数の任意の密な部分環をDとする。つまり、Dは有理数の任意の部分環だが、整数環ではない。ここで考えているのは十進小数（decimal fractions）、つまり分母を10の累乗にして表すことができる有理数だ。D のデデキント切断は、Dの空でない真部分集合 （proper subset）S で以下の条件を満たすものである： x \lt y \land y \in S \implies x \in S 。

これは基本的に [2] でデデキントが定義したやり方である。そして、デデキントは、\{x \in D: x \lt r\} と \{x \in D: x \leq r\} （ r \in D）を同一視する。その理由については、「本質的ではない形で異なるだけなので（only unessentially different）」と述べている。 似たようなやり方として、例えば [8, Definition 1.4] でみられるように、最大要素を持たないデデキント切断に限定して、\{x \in D: x \leq r\} は切断と見なさないという方法もある。なぜそうするのか？実際、 0.\dot{9}は切断\{x \in D: x \lt 1\} に対応し、1は切断\{x \in D: x \leq 1\}に対応する。（一方で、）一般的に、私たちは D の要素 d を切断 \{x \in D: x \leq d\} で識別する。(これを principal cutsと呼ぶ）。 つまり、従来の実数の定義では、 0.\dot{9}=1という式は初めから組み込まれていると言える。だから、この式に挑戦する人は、実は伝統的な実数（traditional real）の正式見解に挑戦していると言えるのである。

ここの伝統的な実数（traditional real）というのは超準実数（nonstandard reals）に対するレトロニムとしての実数だと読める。そして、この後、0^- = \{x \in D: x \lt 0\} を定義している。そして、 0.\dot{9} = 1 + 0^- である。

  • [2] Dedekind, Richard, Continuity and irrational numbers, (1872), in Essays on the Theory of Numbers, Dover, New York, NY, 1963.
  • [8] Rudin, Walter, Principles of Mathematical Analysis, McGraw-Hill, New York, NY, 1964.

他に、このように無限小の要素を定義する分野として超準解析（nonstandard analysis）がある。一般的に先ほどとは逆符号 無限小超実数 0^+ を導入する。そして、この無限小を単に実数に加えれば超準解析ができるというわけではない。ε-Nの代わりに、a_n が a に収束することの表現自体は 無限小超実数 0^+ 無限大超自然数 ω について a_ω-a=0^+ とシンプルに記述できるものの、証明はε-Nよりも難しくなる（cf. RIMS 磯野優介 超準解析入門 の定理 4.7 とその証明を見よ）。ちなみにこの超準実数はアルキメデスの性質を満たさないことが知られている（cf. 非アルキメデス順序体 - Wikipedia ）。

これで

アルキメデスの性質を満たさないものを考えたり、ε-N 論法以外の極限の定義の仕方をしたりすると、別の結論を得られそうなこと

が具体化され、0.999…≠1の世界の入り口に立つことができた。

＜補足的に＞

デデキント切断で最小元最大元ともにあることはないのは、有理数の稠密性が「 a \lt b ならば、ある c \in \mathbb{Q} が存在して a \lt c \lt b となる」と定義されていて、切断の条件を満たさなくなるから。稠密性の証明は、

x \lt y \land x, y \in \mathbb{R} とする。アルキメデスの原理より，n \gt \frac{1}{y−x} となる n \in \mathbb{N} が取れる。これにより，ny−nx \gt 1 が分かる。

再びアルキメデスの原理より， nx \lt m となる m \in \mathbb{N} を取ると， m, m−1, m−2, \dots のうち，nx \lt m' をみたす最小の m' \in \mathbb{Z} が取れる。このとき m'-nx \leq 1 なので，特に nx \lt m' \lt ny が従う。よって，x \lt \frac{m′}{n} \lt yとなって， \frac{m′}{n} \in \mathbb{Q} なので、証明終了。from 有理数・無理数の稠密性の定義とその証明 | 数学の景色

タイプ4が無いことは実数の連続性の定義の仕方の一つであるから、基本的には証明するものではない。例えば、松澤 寛: 解析学の基礎（実数の連続性から定積分の存在まで）では、

これが「数直線には穴がない」ということの数学的な表現でありこれを仮定する．このことから解析学の全ての結果が導かれる．

と表現している。6つの同値な「実数の連続性公理」まとめ（解析学 第I章 実数と連続9） も Weierstrassの公理 「上界を持ち空でない任意の集合が上限を持つ」と同値の表現としてタイプ4が無いことを置いている。つまり、6つの同値な「実数の連続性公理」の1つを公理として置けば、あとは相互に同値性を示すという証明になる。例えば、Weierstrassの公理 を先に置くことで、以下のように示せる。

集合Kの切断＜A, B＞を取ると, 集合Aは上界を持ち, Weierstrassの公理より上限 s=supA が存在する. s∈A もしくは s∉A つまり s∈B かで、タイプ2と3に分かれるが、タイプ4は存在しない。

（ちなみに、逆、dedekind から Weierstrass を導いているウェブ上の証明のもののうち多くになんらかの問題があり、きっちりしているものとしては、 荒牧淳一: 解析学Ⅰ のp6 からの証明がある。）

では、世の中に少なからず存在するタイプ4の不存在を0から証明しているように見えるものを丁寧に見てみよう。どこかに穴があるのだ。

田崎晴明: 実数の構成について は定理13に至るまでの説明はとてもわかりやすい。

ただ、最後の肝心なところを自分で追わないと理解できない。つまり定理13の証明に

α はもちろん A_S か A_L のどちらかに属するが、α が最大値または最小値になることは（上と同様にして）示せる。

（はてなのtex記法の制約で小、大の代わりにS(mall), L(arge) を使っている）という省略があるのだが、対称性から A_L に属するときにそれが A_L の最小値になることだけ示そうとしてみる。最小値でなかったとして、p \lt α \land p \in A_L となる有理数か無理数 p が存在したとする。p が有理数の場合にはそれが、無理数の場合には系 9 (無理数と無理数のあいだには有理数がある) から、かならず p \lt q \lt α \land q \in \widetilde{A_L} となる有理数 q が存在するため q が、α より小さくA_L に属する有理数として存在することになる。これ以上にっちもさっちもいかない。

もう一つ見てみよう。原 隆:実数の構成に関するノート p.20 も似たような手法を用いていてこれが既に q \in A_L に矛盾するとしているが、そこに穴がある。タイプ4の切断なのだから、最小の有理数を仮定しても常にそれよりも小さなある有理数が A_L に含まれるような切断になっていると考えられるからだ。実際 p.21 で、

（注意！）上では「A の上界の最小値」や「A の下界の最大値」があたかも存在するかのような書き方をしたが，これは以下の定理 2.8.3 で証明する．だから，論理の順序を重んじるなら，まず下の定理を証明してから，上の定義で上限や下限を定義すべきなのだ（微積の教科書（田島一郎「解析入門」ではちゃんとそう書いている）．しかしその順序ではかえってわかりにくいと思ったので、敢えて上の順序で書いた．

と書かれている。そのあとで、Weierstrassの公理 を Dedekind の定理 から導いて見せている。つまり、Weierstrassの公理 →（暗黙）→ Dedekind の定理 → Weierstrassの公理 という示し方をしているのでトートロジーだ。

デデキントの公理を無限小の導入によって書き換える、つまりタイプ2と3を区別することによって、他の公理ももちろん成立しなくなる。

また、冒頭で収束の話をしたが、Cauhy列の収束 もここで触れた アルキメデスの性質、デデキントの公理、Weierstrassの公理 に加えて、実数の連続性の公理の１つである。ただ、収束とは何かということを持ち込んでいるので一つ余分な前提が入る。詳しくは 【微分積分学】コーシー列とは～定義と収束性の証明～ | 数学の景色 を参照。

＜その先を考えてみる＞

  • 超準実数とWeierstrassの公理はどのような関係にあるだろうか。
  • 関数の微分も影響を受けるだろう。微分はどのように再構成されるだろうか。
  • 超準実数は何を満たさないのか。ゼロ元との積がゼロになるとは限らないとかかはそうだよね。

ここらへん説明できる人はぜひぜひトラバとばして（古い！）ブログを書いてください。

＜その他参考＞

  • 桂田 祐史：数学解析 で、定理1.14アルキメデスの公理を、Weierstrass の公理から示している。
  • 選択公理と同値なツォルンの補題と非常に似た形をしてて何か関係あるかなと考えたけれど、「半順序集合Pは、その全ての鎖(つまり、全順序部分集合)がPに上界を持つとする。このとき、Pは少なくともひとつの極大元を持つ。」 は全順序集合について、「全順序集合Pは、その全ての部分集合がPに上界を持つとする。このとき、Pは最大元を持つ。」 となって、切断点でもそれより大きい場所でもどこかに恣意的な上限を設定しないと、前件を満たさないので適用できないので、関係が無かった。

■

消費者庁が「アイリスオーヤマ」「BRUNO」偽サイトに注意喚起…“巧妙なつくり”に騙されないポイントを聞いた

これ、クレカの情報入力する画面まで試したんだけどかなり巧妙で難しいなと思った。

1つ目は、URLです。公式サイトとURLまでよく似ています。
2つ目は、通販サイト全般に言えますが、価格です。実態の価格にに比べて格安の販売価格が表示されています。
3つ目は、支払い方法。支払い方法が、クレジットカード決済のみであることです。

ダメだと思うこの判断基準。

URLも、ドメインって概念を知らないと判別できないけど、whois やれば怪しさがわかった

f:id:cm3ak:20220324230208p:plain

ssl は接続先までの経路を安心するためのもので、接続先の安全さは保障してくれないってのは基本中の基本だけど、今回もCloudflareを使ってウェブサイトを無料でHTTPS化してるっぽいね。

2つめ、3つめは、格安でもないちょっと安めを提示したり、他にも詐欺しやすい決済方法を用意したりすりゃあいいだけなので、こんなの判断基準として提示しちゃいけないと思う。

all rights reserved のところが「全著作権所有」になっていたり（思わず末尾 suoyou って読んじゃったｗ）まあこういう怪しさがまだ少しは残ってるんだけど、商品の比較とかもふくめて、機能を作りこむのにおそらく日本円で10万くらいしかかかってないのかもしれない。そこで100万詐欺できたらとりあえず儲けって感じかな。サイトを作るところのコストの低下がこういうのが出現し始めた原因なんだと思う。ドメインの来歴を保障し簡単に確認できる仕組みがウェブに必要になってきてるんじゃないかなぁ。

前順序の場合に最大元は存在すれば極大元や上限になるか？

まず最大元の定義は、前順序(Q, \preceq)とその部分集合 P \subset Qについて以下。

g=Greatest~element(P, \preceq ) \overset{\text{def}}{\iff} g \in P \land \forall y \in P (y \preceq g)

b \in P に対して g \preceq b とする。g は P の最大元なので b \preceq g である。

一方で、極大元 m の定義は以下である。

m=Maximal~element(P, \preceq ) \overset{\text{def}}{\iff} ( \exists m \in P (\exists y \in P (m\preceq y) \implies y \preceq m ) )

m を g に、y を b に読み替えるとこれを満たしていることが分かるので、前順序でも最大元は存在すれば必ず極大元になる。

また、上界 u は

\exists u \in Q (\forall y \in P (y \preceq u))

その最小元である上限 s は、上界の集合 R \subseteq Q について、

\exists s \in R (\forall y \in R (s \preceq y))

g \in P, s \in R および上界の定義から、g \preceq s。また、 g \in R および先ほどの上限の上界内での最小性より、s \preceq g。

しかし、先ほどと違い、ここから s = g が言えない限り最大元が上限になるとは言えず、それが言えない（反対称律が成立しない）ことが前順序の特徴であるので、少なくともこの手順では最大元が上限になるとは言えないことになる。「半順序ではなく前順序であること」は反対称律が必ず成立するわけではないこと、つまり、１つ以上成立しない場合があることしか言っておらず、最大元が上限になる可能性はある。ただ、上の s と g について反対称律が成り立たない場合に最大元が上限でないことは自明であり、この反例が存在する限り、前順序を考慮すると最大元は上限のサブクラスではない。

Wikimedia Community Wishlist Survey 2022 で上位50位に入った Wikidata 関連の改善項目

Wikidata

Community Wishlist Survey 2022/Results より。

13位: Autosuggest linking Wikidata item after creating an article

Wikipedia の異なる言語間のページ同士、Wikipedia と Wikidata の既存項目が適切につなぎ合わされずに別々の項目として作られてしまうことがある問題。Wikipedia の記事を作成した後に、同名・類似名のWikidata 項目をリンクするよう案内するポップアップが表示される。ユーザはそれがリンクに適しているかどうかを判断し、適切なものが無ければ Wikidata 項目を新しく作ることになる。

37位: Custom edit summaries

Wikidata は Wikipedia と違って編集メモを人手で書くことができなかった。それをできるようにする。

49位: Corresponding properties

親子関係や夫婦関係など、片側の情報を入れたときに「逆方向の情報も入れますか？」というプロンプトを出して、ユーザがOKすることで、簡単に inverse property を入力するようにする。

メルロポンティ再挑戦してみた

「挑戦」って言葉を使っているのは、

とか書いてた通り、鷲田 清一: メルロ=ポンティ (現代思想の冒険者たちSelect) を読んでマジでわからんかったという印象があったからで、友人に「メルロポンティがわからんなんてショック…」とか言われてある程度解説してくれることも約束してくれたので、再挑戦してみようと思ったのだ。加賀野井 秀一: メルロ=ポンティ 触発する思想 (哲学の現代を読む) を読んで、この本はシリーズとして 、

哲学者の些末な生涯など、きれいサッパリ切り捨てて、直接、テクストの「読み」から出発する

というポリシーがあるにも関わらず、次のメルロポンティ自身の言葉を引きながら、彼の思想を生涯から切り離すのは難しいとして彼自身にもフォーカスしながら書かれている。

この場合、〔歴史なら〕歴史というものを、イデオロギーから出発して了解すべきであろうか。それとも政治から、それとも宗教から、それとも経済から出発して了解すべきであろうか。また〔一つの学説なら〕学説というものを、その表明された内容から了解すべきであろうか。それとも著者の心理や彼の生活上の出来事から了解すべきであろうか。ほんとうは、同時にあらゆる仕方で了解せねばなあらぬのであって、すべてが一つの意味をもっており、われわれはすべての諸関係のもとに同一の存在構造を見出すのである。以上に挙げたどの見方も、それらをバラバラにしてしまうのでなければ、また、歴史の根柢まで降り下って各展望の中に顕在化されている実存的意味の独自の核に到りつきさえすれば、すべてが真実なのである。

from p.24 、元は『知覚の現象学』１ー１９６７年翻訳本ⅩⅣページ。このことには半分同意するが半分同意しない。つまり、メルロポンティ研究をするのならばこの態度は正しいだろう。しかし、僕はその成果からくる、「ある程度彼を理解した」と思っている人たちの理解の平均が得たい、今回においては少しわかったら良いのであって、さして彼に興味があるわけではない。一方で、それぞれの著作の成立背景ぐらいは読み解きに役立つ。『見えるものと見えないもの』はもともと遺稿であって、グザヴィエ・ティリエット（Xavier Tilliette） が「メルロ＝ポンティが教育と研究とを厳密に区別していたという事実、彼が確実な成果を提示しようとし、自分のひそかな準備作業に他人を巻き込むのを好まなかったという事実」から、これが出版されたものと文体を大きく異にすることになったと解しているように、それまでの著作とは違い、説明がまとまっておらず、独自用語だらけで、よりポエティックらしい（p.266）。僕が理解できないとツイートしていた炸裂や肉の話などはこの作品にでてくるので、そもそも理解は後回しで良いと思える。「裏返しになった手袋の指」などという僕をメルロポンティアレルギーにした手袋メタファーもここに出てくるのだ。

以下、いくつかメモを小項目に分けて書く。

「キリスト教とルサンチマン」の話は無視でいい気がする。

初めの論文「キリスト教とルサンチマン」において、ニーチェの『道徳の系譜』の話をマクス・シェーラーを援用して、「意識に現れるすべてのものが生理的かつ生命的な因果性の直接的あるいは間接的な産物であると認めることは、根拠のない公準に過ぎない」（p.56）と言っているが、これ自体はそもそも「『道徳の系譜』はそんな話だったっけ？」とも思うしピンとこないということに友人も同意してくれ、この本では、『行動の構造』の解説のところで

革命の減少や自殺行為が、人類にしかないものだということは、しばしば指摘されてきた。それは、両方とも、与えられた環境を拒否し、環境全体を越えたところに平衡を求めようとする能力を前提とするからである。かの周知の保存本能という概念は、これまでかなり濫用されてきたけれども、そういう本能は、人間においては、おそらく病気とか疲労の場合にしか出現しないものであろう。健康な人間は、生きることを求め、世界における、また世界の彼岸の或る対象に到達することを求めるのであって、自己の保存を望むものではない。

という１９６４年翻訳本２６２ページを引いてきて、

本来、健康な人間は、高い統合度を実現しており、自己保存のみに汲々とすることはなく、時には自己犠牲すら厭わず、彼岸的価値を求めることもある…。いかがだろう。これはまさに、あの「キリスト教とルサンチマン」で展開されていたニーチェ批判を髣髴とさせるものではあるまいか。

（p.99）と言っているけれど、ニーチェの術語としての健康概念と、メルロポンティの一般的な健康概念を混同して考えてるように見えてしまう。私なりに整理しておくと、ニーチェはルサンチマンにとらわれたような病的な状態がキリスト教道徳のもとになっているのではと言っていて、メルロポンティは、健康な人間ほどキリスト教道徳のような道徳を持ちうると言っているから反対だと考えられるという話のようだが、ここの健康/病の区分けが異なっているので批判になっていないというわけだ。

道徳における奴隷一揆は、ルサンチマンそのものが創造的となり、価値を生み出すことから始まる。［...］あらゆる貴族道徳は自己自身への勝ち誇れる肯定（Ja-sagen）から生まれ出るのに対して、奴隷道徳は始めから〈外のもの〉・〈他のもの〉・〈自己ならぬもの〉に向かって否（Nein）と言う。この否こそが、その［奴隷道徳の］創造的行為なのだ。（KSA, 5, S. 270f.）

―私は一つの原理を定式で表わす。道徳におけるあらゆる自然主義、言いかえれば、あらゆる健康な道徳は、生の本能によって統治されている［...］。反自然的道徳、言いかえれば、これまで教えられ、敬われ、説かれてきたほとんどあらゆる道徳は、逆にまさしく生の本能に背いている、―それはこの本能をときにはひそかに、ときには厚かましく断罪している。（KSA, 6, S. 85.）

ニーチェにおける道徳批判:欲望と理性の関係 から孫引きしておくとこんな感じなんだから。

双方向性および図-地構造

『行動の構造』から『見えるものと見えないもの』に至るまで頻出の概念は知覚が双方向的に生じるものであるというコトである。

たとえば私の右手が私の左手に触れるとき、私は左手を「物理的な物」として感ずるが、しかし同時に、私がその気になれば、まさしく、私の左手もまた私の右手を感じはじめる

from p.273 『シーニュ』２ー１９７０翻訳本14-15ページ

青色は、私に或るまなざし方を求めるところのものであり、私のまなざしを一定の運動によって触れてみることのきるものである。それは私の眼と能力、そして私の前身の能力に差し出される或る領野もしくは或る雰囲気なのである。

from p.277 『知覚の現象学』２ー１９７４翻訳本13ページ

たとえば、あの有名な「ルービンの盃」を考えてみよう。古典的反射学説からすれば、対象から与えられる刺激は同じはずなのに、私たちはそこに「盃」を見ることもできれば、「向かい合った二つの顔」を見ることもできる。つまり主観は対象によって一義的に決定されてはいないのだ。けれども、そうかと言って私たちは、この図の中に馬や羊の姿を勝手に見て取ることはできない。つまり、主観が対象によって制約されていることもまた真実なのである。

from p.82-83

すでにルービンの盃の話で一部みてとれるが、これらの双方向性にはいくつかのやりかたで説明できる「構造」が介在している。手と机の方向性について、

もちろんここで論じられているのはアナクロニックな物活論ではあり得ない。

p.276 といっているが、メルロポンティは物活論っぽさがそこかしこにあるんだよなぁ。それが嫌い。

＜ゲシュタルト＞

私たちは点的な刺激をバラバラに受け取るのではなく、刺激はすでに、ある一つの「形態（ゲシュタルト）」として私たちに働きかけてくるのではないか。そしてこのゲシュタルトこそが、ベルクソン流に言えば、「意識への直接与件」なのではあるまいか…資料を参照すればするほど、メルロ＝ポンティにはそう思われてきたのである。

たとえば、ある唄を耳にするような時、私たちは、高度に訓練された音楽家でもないかぎり、決してそれを正確な音階として記憶するわけではないだろう。個々の音よりも前に、まずは、全体的なゲシュタルトがある。だからこそ私たちは、たとえ正確な音程はとれずとも、おおよそのメロディーを再現することができるのではないか。

p.78-79

このゲシュタルトの統合度について　物理的秩序／生命的秩序／人間的秩序、癒合的形態／可換的形態／象徴的形態といった区分けを用いて『行動の構造』の中で体系化しているがあまり参照するに値する概念ではないと思ったので割愛する。それらの説明は上記からp.96くらいにかけて説明されている。

＜内部地平と外部地平＞

こうした「地平」は、『経験と判断』あたりになれば、フッサールによってさらにはっきりと「内部地平」と「外部地平」として表現されるようになるが、いずれ基本的な発想は変わらない。難破船を規準とすれば、その「帆柱」、「帆柱に刻まれた文様」、「文様に彩色された塗料」…といった系列が内部地平、難破船を取り囲む「砂丘」や「森」、そのすべてを含む「渚」、渚を含む「海岸」、さらには、その海岸をも含む「ランド地方」…といった系列が外部地平となるだろう。つまりここでは、ある知覚対象を出発点として、その内部にも外部にも無限に探索の目を向けることができるという地平構造が語られているのであり、究極のところ、あらゆる地平を包括する地平は、この世界の全体、フッサール言うところの「生世界 Lebenswelt」となるわけである。

p.124-125

この２つの構造は黒板にチョークで書いた〇が〇としてどう認識されるかとか考えるとシンプルで分かりやすいと、僕は思っている。

＜図ー地　構造＞

それはちょうど、カメラのファインダーを覗きながら、あちらこちらに焦点を合わせるようなもので、「図」と「地」は互いに移行し合いながら、浮かび上がったり沈み込んだりするのである。

知覚とは、このように「図」と「地」の双面をともなう行為なのであって、「図」のみに直接対応するものではあり得ない。「図」が「図」として存在するのは「地」あればこそ。「図」も、その「図」の「意味」も、ひいてはそれらがこぞって指し示す「事物」の存在も、すべては「地」という他なるものを経由して初めて到達されることになるわけだ。これを「差異化作用」と呼んでみてもよろしかろうし、そこに「間接的存在論」の萌芽を感じ取るのもよろしかろう。

p.120

自己の身体とは、図と地という構造にいつも暗々裡に想定されている第三の項なのだ。

p.130 『知覚の現象学』１ー１９６７翻訳本１７６ページ。

手袋再訪

可逆性(reversibilite)

手袋を裏返すと、指先の何もなかった空間に裏返された手袋が存在する。つまり手袋の意味は、手袋の表裏が密着した折り返し点に生成している。あらゆる物事は、内と外が接し織りなす、リヴァーシブルな「襞」にしか存在しないのだ――。これがメルロ=ポンティの「可逆性」である。意識でも物体でもない存在として人間をとらえる「両義性」の思考を、両者の相互交流という視点から深めることで到達したこの考え方により、存在論のあらたな地平は切り拓かれた。そして哲学的反省は閉じた系として完結することを禁じられ、現象学のアクチュアリティは無限に拡大する。

手袋の話はルービンの盃と同じだ、と友人が言ってくれたので、そこは分かった。内と外が云々というのはメルロ=ポンティではなくフッサールの方で＜内部地平と外部地平＞の話で僕は理解できた。意識でも物体でもない存在として人間をとらえる「両義性」については、あまり深く言及しなかったゲシュタルトの統合度の話で理解できた。まあ、なんとなく再挑戦に値するだけの成果が得られたのではないだろうか。

ここまで触れた章で全体の1/2で、『ヒューマニズムとテロル』から『弁証法の冒険』へ、『シーニュ』、『眼と精神』については図書館で借りた本の返却期限にて時間切れで読んでいない。ところどころフランス語カタカナ読みでルビがふってあって、たとえば「一歩一歩（パザパ）」といった具合で、それを pas à pas と変換し「駆け足――ジャック・デリダにおける脱構築と政治の速度 」みたいな文書にたどり着いて文脈を知るといった感じで、元々デリダを知っていたら分かるとかはあるんだろう。僕はデリダも避け気味。p.120 の「差異化作用」の言及とかはソシュールかとか、そういうのも知ってればわかるね。

ゲシュタルト心理学については 57歳で博士号を取得して、日本語学界に多大な影響を与えた男【三上章2】#100 - YouTube で、エドワード・サピア（Edward Sapir, 1884年1月26日 - 1939年2月4日）や三上 章（みかみ あきら、1903年1月26日 - 1971年9月16日）も触れていたという話が挙げられているが、20世紀初頭、本当に多大な影響力を持っていたことが分かる。

遺稿以外を理解したと思ったら、欲が出て、遺稿についても再挑戦してしまった。＜肉＞の存在について : メルロ=ポンティ後期哲学における「可逆性」の意味 : HUSCAP と後期メルロ=ポンティ哲学における可逆性と他性を通読した。

まず初めに思ったことは、やはり遺稿は遺稿以外をベースに理解されなければならないということだった。つまり、前者の論文で再検討されている他者やコップの両義性は、上の双方向性の話から、ほぼ一歩も出ていないとさえいえる。コップはゲシュタルト統合度においても、他者は少なくともその他者性によって、ある種のたどりつけなさがある。その「たどりつけなさ」をこの論文では「同一ではない」と表現している（p.209 「私の手が他者に触れられると他者が私に触れるとは、可逆的だとしても、同一のことではないのである。」）が、ならば可逆（réversibilité）なんて言葉がそもそもミスリーディングだし、右手と左手という直観的にも可逆な例を代表にしているのもミスリーディングだ。

後者の論文では「メルロ=ポンティの哲学には他者の他性の観点が欠けているとは、多くの論者の指摘するところである。」（p.276）なんて言われてるし、 真に何を意味しようとしていたかはさておき、少なくとも適切な言葉選びではない。 「常に切迫 (imminente ) してはいるが、事実上決して実現されない可逆性が重要なのである。」 (p.277からの孫引き）と言っているが、その実現されなさに関する説明はほとんど完成されていなかったそうだ。冒頭私のツイートで図示したように、双方向の図と地が生まれる前の状態として＜肉＞（chair）が想定され、それが裂けて（éclatement）図と地が生まれる。「他性は二項関係の外部に、「第三項」として出現しするのではない。むしろ他性とは、可逆性の切迫によって、まさに二項関係そのものを炸裂させ、瓦解させるものである。」（p.285）とあるのは半分同意する。同意しない半分を説明すると、他性が＜肉＞を裂くのではなく、それが無意識であるにせよ、認識が＜肉＞を裂き、他性を生むのではないかと思う。それでは、デカルトに逆戻りじゃないかという言われそうな気もするが、認識に存在が必要であることはその通りで、その主体-認識-対象は atomic*1であって、主体は主体と呼ぶに値せず、対象は対象と呼ぶに値しない。それが atomic であるからこそ、対象を対象として取り出そうとするときには三角測量のようなテクニックが必要なのである。

*1:それ以上分割できない最小の単位、という意味で使っているが、あまり一般的な英語の用法じゃないらしい…。individual も違うし、indecomposable も直既約としてよく使うし、…日本語で最小単位とでもしておけばよかったか。